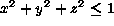検索, 亀田能成, 美濃研, 総合情報メディアセンター

三次元物体の表現

計算機上で三次元世界を表現する以上、三次元物体も計算機上のデータ構造で 表現しなければならない。三次元物体の表現法は、大きく分けてソリッドモデ ルとサーフェスモデルがある。ソリッドモデルは物体を三次元で表す。例え ば、単位球を表現する場合、ソリッドモデルではこれを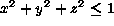 で表現する。ソリッドモデルを表現するには関数モデルや離散モデル（ボクセ ルという単位立方体の集合で表す方法など）などがあり、一部のCADなどでの 試作シミュレーションや科学技術計算などによく用いられる。しかし、CGに限 った場合、物体内部の属性は不要であり、その表面についてのデータだけを考 慮するのがサーフェスモデルである。

サーフェスモデルの場合にも、その表現形態には関数モデルと離散モデルがあ る。関数モデルはパラメトリック曲面を構成するもので、ベジェ曲面や B-Spline面、さらにその発展形であるNURBSや、メタボール、超二次関数、さ らにはフラクタクル関数に代表されるようなファンクショナルモデリングもこ の範疇に属する。これらはその属性を踏まえれば数少ないパラメータで曲面を 制御でき便利であるが、その一方で各々の関数形式を越えた曲面を表現するこ とは困難である。一方、離散モデルは一般にポリゴンモデリング、パッチモデ リングと呼ばれている手法で、ある実際の曲面を微小な多角形の面の集合で表 現するものである。理論上は面を微細にしていけばどのような面でも十分な精 度で近似できるという利点を持つが、他方でそのパラメータ数は膨大（原則的 に頂点の数の変数）になるという欠点をもつ。現在の計算機環境で は汎用性に富むポリゴンモデルが支持されていることが多い。これは、優秀な レンダリングアルゴリズムとハードウェアの出現によるところが大きいと思わ れる。

本演習では、三次元物体の形状を表すために、オープンな規格の一つである VRML ver 1.0の構文の一部を利用する。

本演習で最低限用いるフォーマットは以下のみである。

• Material
  • ambientColor
  • diffuseColor
  • specularColor
  • shininess
• Coordinate3
• IndexedFaceSet

VRMLのファイルはテキストファイルであり、通常拡張子がwrlである。次にサ ンプルを示す。

#VRML V1.0 ascii

Material{
	diffuseColor    1.0 1.0 0.0
}

Coordinate3{
  point [
    0.0     1.0     2.0,
    2.0     0.0     3.0,
    2.0     2.0     2.0,
    1.5     6.0     0.5,
    1.0     0.0     0.0
  ]
}
IndexedFaceSet{
  coordIndex[
    1, 2, 4, -1,
    0, 2, 3, -1,
    0, 4, 2, -1
  ]
}

Coordinate3ノード内のpointフィールドのカンマで区切られたセットが一つの 頂点の座標を示している。頂点番号は、一つ目から順に番号と なる。IndexFaceSetノード内のcoordIndexフィールド内の各インデックスは-1 で区切られ、それぞれCoordinate3の頂点の番号を組み合わせて一つの面を表 現している。一行目の例では、頂点1と頂点2と頂点4とでできる三角形の面を 表す。

本演習では、この頂点の並びによって面の裏表の区別をつける。すなわち、頂 点の並びが反時計回りに見える側が表（法線方向）であるとする（これは VRML 1.0の規定ではない）。VRML 1.0ではポリゴンが多角形でも構わない が、問題を簡単にするため、本演習ではポリゴンは全て三角形であるとする。

Matrialノードについては各フィールドの意味はシェーディング処理の項で詳 しく述べるが、各フィールド（上記の例ではdiffuseColor）に続いて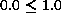に正規化された(R,G,B)の値で色を表現する。ただし、shininessだ けは１要素のみが後に続く。