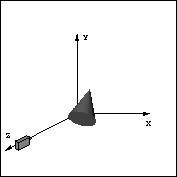
図 1: 三次元世界中の物体とカメラ
検索,
亀田能成,
美濃研,
総合情報メディアセンター
私たちが三次元世界を視るとき、その情報は目の水晶体を通し網膜上に結ばれ た像から得ている。基本的にはカメラの撮像原理も同様である。このような撮 像系として代表的なものに、並行投影と透視投影がある。
まず、三次元世界全体を考えよう。三次元世界を表現するために、三軸の直交 座標系を採用する。その軸は右手系の順序でX,Y,Zとする。そして、その世界 の中には物体が存在する。(光源も存在するが、ここでは幾何的な問題に集中 するために考えない。これについては7章で述べる。)
三次元世界の画像を生成するとは、この三次元世界を二次元平面に投影変換す る問題に他ならない。ただし、得る画像の大きさは有限なので、投影する際に 空間のどの部分を投影するかを意識する必要がある。以後、この投影される平 面のことを画像平面と呼ぶ。
また、これ以降は座標系は同次座標系![]() で表現する。同次座標系は空間を表す三要素のベクトルに一要素を加え
たもので、空間の射影問題を解くときに都合が良い。三次元ユークリッド空間
上の一点
で表現する。同次座標系は空間を表す三要素のベクトルに一要素を加え
たもので、空間の射影問題を解くときに都合が良い。三次元ユークリッド空間
上の一点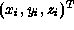 は同次座標系では
は同次座標系では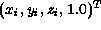 で表現で
きる。また、同次座標
で表現で
きる。また、同次座標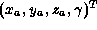 は各要素を
は各要素を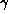 で割れ
ば、その三次元ユークリッド空間上の点の位置となる。
で割れ
ば、その三次元ユークリッド空間上の点の位置となる。