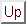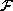 has the parts whose rotation angles have been
determined and a set
has the parts whose rotation angles have been
determined and a set 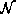 has the parts whose parent part belongs
to
has the parts whose parent part belongs
to  . The rest parts belong to a set
. The rest parts belong to a set  . At the beginning
. At the beginning
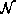 only contains the root part and all other parts are in
only contains the root part and all other parts are in 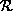 .
.
Kameda,
Research,
Documents and Info


In this section, we describe a contour based algorithm to estimate a pose of the articulated object. This algorithm uses the definition of the model, but does not use the values in the model so we can easily change the target object without modifying the algorithm.
Each part in the model is taken up one by one and its rotation angles are determined based on the overlap relationship between the contour of the silhouette and that of the projected region on the image plane.
Suppose a set 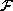 has the parts whose rotation angles have been
determined and a set
has the parts whose rotation angles have been
determined and a set 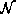 has the parts whose parent part belongs
to
has the parts whose parent part belongs
to  . The rest parts belong to a set
. The rest parts belong to a set  . At the beginning
. At the beginning
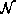 only contains the root part and all other parts are in
only contains the root part and all other parts are in 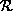 .
.
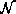 . If there is no part in
. If there is no part in 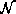 , the
algorithm terminates. Make a new candidate-list for Part i. A
candidate in the candidate-list represents a possible pose of Part
i, and has at most three rotation angle values which are quantized
by a certain unit interval. The unit size defines the resolution of
the pose estimation. A candidate can not have values that make the
projected region of Part i stray out from the silhouette. If there
exist no candidates in the candidate-list, go to Step
3.
, the
algorithm terminates. Make a new candidate-list for Part i. A
candidate in the candidate-list represents a possible pose of Part
i, and has at most three rotation angle values which are quantized
by a certain unit interval. The unit size defines the resolution of
the pose estimation. A candidate can not have values that make the
projected region of Part i stray out from the silhouette. If there
exist no candidates in the candidate-list, go to Step
3.
 to
to
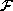 , and the children of Part i in
, and the children of Part i in  are moved to
are moved to 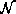 . Go to Step 1.
. Go to Step 1.
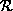 . For Part j,
execute the same algorithm as Step 2. Go to Step
1.
. For Part j,
execute the same algorithm as Step 2. Go to Step
1.
Since it is not clear what kind of criterion is necessary to select the part in Step 1, our method here selects it arbitrarily. We are currently investigating this problem.