検索, 亀田能成, 美濃研, 総合情報メディアセンター

ラスタライズとクリッピング

空間上の三角形ポリゴンは、3章の投影変換により画像平面 上の三角形に変換される。これを実際に画像上に描画するためには、この実数 表現である画像平面上の三角形を量子化された画素に変換しなくてはならな い。これを実現する方法は幾らでも考えられるが、商業性を考慮する場合は、 リアルタイムCG表示システムを念頭におくと、ハードウェア構成設計やその高 速化を意識したアルゴリズムにする必要がある。つまり、単純な計算に分解し やすいアルゴリズムや並列性の高いアルゴリズムを考えることが、チップ製造 の容易さや高速性への適用性に結び付くのである。

本実験では、これをラスタライズとクリッピングという技法を用いて実現す る。これがなぜ商業性を考える上で有利なのかは各自プログラム作成を行いな がら考察してもらいたい。

さて、三角形を画素に分解するのがラスタライズで、これは１画素が画像平面 上の三角形に対してどれほどの大きさになるかを計算し、三角形をX軸方向に 沿ってラスタ分解するものである。このX軸方向に沿った１列をスキャンライ ンという。さらに、スキャンラインごとに描画画素を決定する。

ラスタライズを簡単にする一つの方法は、画像平面上の三角形の頂点をY座標 の値によってソートし、真中の値をもつ頂点によって三角形を二つに分割する 方法であろう。図4において、三角形ABCを三角形ADBと三角形 CDBに分解する。

  
図 4: 三角形のY軸方向の分解

  
図 5: 三角形のラスタライズ

各三角形ADB,CDBの各頂点の座標の計算は透視投影（並行投影）で計算でき る。また、図5の辺PQ上の点Rの値は頂点どうしの内分比によっ て簡単に求められる。この辺PQがスキャンラインである。点Aの座標を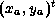などと表すと、計算式は以下のようになる。

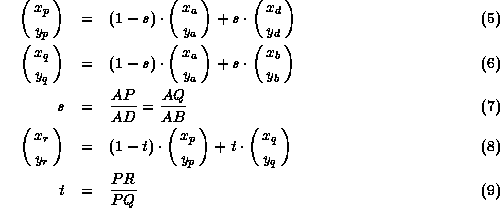
また、この画素計算において、画像の大きさを保持しておいて、一部が画像か らはみ出すようなポリゴンの場合には、画像からはみだす部分については処理 を行わないようにする。この処理をクリッピングという。

なお、本章での実数表現の三角形を量子化された画素上へ変換する処理は、工 夫を凝らさないと一般にジャギーといわれる現象を引き起こす。本演習では学 生の諸君はジャギーの発生に対して対策を施さなくともよい。